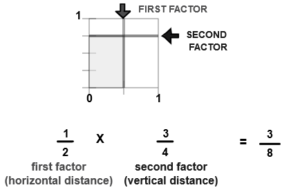
What is the Rational Number Between 1/4 and 1/2? The density property states that between two rational numbers there is another one. So, if a number is between 0 and 1/2, the rational number in between those two numbers is 1/4. Therefore, the rational number between 0 and 1/2 is 2/8. Similarly, a rational number between 2/4 and 1/2 is 3/4. The denominator of these two numbers is the same. However, you cannot write the rational number between these two numbers.
The number between 0 and 1/4 is the rational number between these two numbers. But, there is another one between 1/4 and 1/2 that is not a rational number: 1/64. That is, it is 7/24. And the rational number between 1/4 and 1/2 is 3/8. But, if you put these two numbers in a number line, they will appear to be non-coordinated.
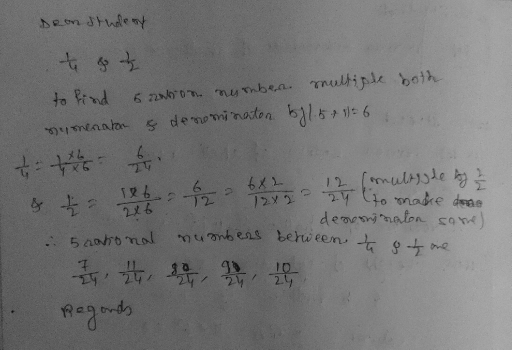
If you want to find the rational number between 0 and 1/4, you can use the average of the two numbers. By adding 0 and 1/4, you can get the rational number between 1/4 and 1/2. Then, multiply this number by four to get the answer. If you want a rational number between 0 and 1/4, you can multiply it by four. For a rational number between 1/4 and 1/2, the answer is 1/4.
Similarly, the rational number between -5/11 and -6/7 is -27/35. The rational number between -5/11 and -6/11 is -29/56. This number also lies between -2/7 and 3/4. Moreover, it is -1/11 and -10/11, whereas the rational number between 3/11 and 6/7 is 29/35. Once you know the answer to these questions, you can move on to other problems.
A rational number is a fraction in which the denominator is not zero. In other words, a rational number is a fraction of a decimal number. The denominator must be greater than zero. When a rational number is divided by a fraction, the result is a decimal number. This is the result of the division of the rational number. You can divide the number by this denominator.
What is the Rational Number Between 1/4 and 1/2?
Rational numbers are those that can be expressed as a fraction, where the numerator (top number) and denominator (bottom number) are both integers. In other words, rational numbers are fractions with whole number values.
The rational number between 1/4 and 1/2 is 3/8.
Rational Numbers what are they?
Rational numbers are those numbers that can be expressed as a fraction p/q, where p and q are integers and q is not equal to zero. In other words, rational numbers are numbers that can be written as a ratio.
Whole numbers are rational numbers because they can be written as a fraction with a denominator of 1. For example, the number 5 can be written as 5/1.
Integers are rational numbers because they can be written as a fraction with a denominator of 1. For example, the number -5 can be written as -5/1.
Terminating decimals are rational numbers because they can be written as a fraction with a denominator that is some power of 10. For example, the number 0.75 can be written as 3/4 or 75/100.
All repeating decimals are rational numbers because they can also be written as fractions. For example, the decimal 0.333…can be written as 1/3 or 10/30 or 100/300, etc
How do you find a rational number between two numbers?
When you’re looking for a rational number between two other numbers, there are a few things to keep in mind. First, remember that a rational number is any number that can be expressed as a fraction, with both a numerator and denominator. Second, the two numbers you’re looking for a rational number between don’t have to be whole numbers, they can be any two numbers.
To find a rational number between two numbers, start by finding the midpoint between the two numbers. To do this, add the two numbers together and then divide by 2. This will give you the average of the two numbers. However, this isn’t necessarily a rational number (for example, if the two original numbers were 1 and 3, the midpoint would be 2 but 2 can’t be expressed as a fraction).
If the midpoint isn’t a rational number, pick one of the original numbers and then find the halfway point between it and the midpoint. Continue doing this until you find a rational number that lies between your original two numbers.
What is a rational number between 1/2 and 1?
A rational number is a number that can be expressed as a fraction, where both the numerator and denominator are integers. In other words, it is a number that can be written in the form of a ratio.
All integers are rational numbers, since they can be expressed as a fraction with a denominator of 1. For example, 3 can be written as 3/1, which is a rational number.
When we talk about rational numbers between 1/2 and 1, we are referring to fractions where the numerator is less than the denominator. In other words, these are numbers that are less than 1 but greater than 1/2. Some examples of rational numbers between 1/2 and 1 include 3/4, 4/5, and 5/6.
These numbers can be helpful in many situations. For example, if you are trying to find a number that is halfway between 1/2 and 1, you could use the rational number 3/4. This number is exactly halfway between 1/2 and 1.
Are there any rational numbers between 1/3 and 1/2?
There‘s a lot of debate on this topic, but it ultimately comes down to whether or not you believe that 1/3 and 1/2 are rational numbers. If you believe they are, then there‘s no reason why there couldn‘t be another rational number between them. However, if you don‘t believe they‘re rational numbers, then there can‘t be any other rational numbers between them.
What is the rational number between 0 and 1/2?
There is an infinite number of rational numbers between 0 and 1/2. To find one, simply take any number between 0 and 1/2 and divide it by 2. For example, 1/4 is a rational number between 0 and 1/2.
How to find a rational number between two irrational numbers?
It can be difficult to find a rational number between two irrational numbers, but there are a few methods that can help. One way is to use the continued fraction method. This involves taking the two irrational numbers and writing them as fractions. Then, take the reciprocal of each fraction and add them together. The result will be a rational number between the original two numbers.
Another method is to use the mean-value theorem. This states that if two points on a curve are taken, then there exists a point on the curve between them such that the tangent line at that point passes through the points. This can be applied to finding a rational number between two irrational numbers by graphing them as points on a curve and then finding the point between them with the desired property.
Both of these methods can be used to find a rational number between any two irrational numbers. With some practice, it can be relatively easy to do this.
What is the rational number between 1 and 2?
The rational number between 1 and 2 is 1.5. This is because it is halfway between the two numbers.
Conclusion
We hope this blog post “What is the Rational Number Between 1/4 and 1/2?” has helped clear up any confusion you may have had. If you have any further questions, feel free to reach out to us and we would be happy to help!
Today sponsors are Pinson Well Logging and Mailbox Repair Tulsa