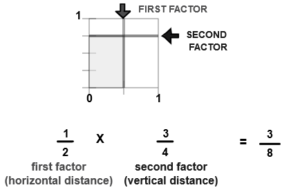
How to Know When to Give an Answer in Fractions Or Decimals?

How to Know When to Give an Answer in Fractions Or Decimals? There are several ways to write a fraction, including dividing by the number in the denominator, and then writing the answer in decimals. Regardless of the method, always note the decimal point. Once you have written your answer, you can either move on to the next question or click on the “review” button to see how the answer was derived. This method will allow you to easily understand your answer, even if you’re not a math genius.

In general, a question asking “How to know when to give an answer in fraction or decimals?” requires the answer to be presented in either fractions or decimals. Fractions with multiples of 10 should be answered in decimals. The denominator in an equivalent fraction is always one with a single zero, a decimal, or both. The answer can be given in either format, and the process can be repeated to find the decimal equivalent of a fraction.

Every non-whole number is represented by a fraction. The simplest way to convert a fraction to a decimal is to divide the numerator by the denominator. This is done by using a calculator. The calculator will give you the value of the fraction as a decimal. You can also use a calculator to convert a fraction into a fraction.

Another important tip is to learn to distinguish the difference between percentages and decimals. If you are not sure which is more correct, a quick Google search will help you understand what the difference between percentages and decimals is. Decimals are easier to convert to fractions, so this strategy is often the best choice for many students. It also makes a good sense to understand how decimals and percentages work together.

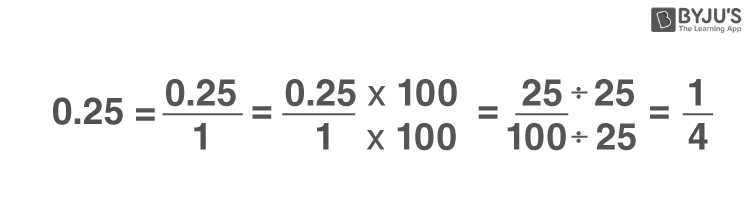
Knowing how to operate fractions is essential for your students to succeed in math. They provide the basis for decimals and percents, which students can use for proportions, slopes, and rational numbers. Without mastering the fundamentals of fractions, students struggle to understand other math concepts, putting their learning at risk. Besides, students who don’t master fractions often fall victim to tricks and are more likely to use the wrong method for a problem.

How to Know When to Give an Answer in Fractions Or Decimals?

When it comes to fractions or decimals, there is no one-size-fits-all answer. The key is to understand when you need to be precise and when you can round off. Here are some guidelines to help you know when to give an answer in fractions or decimals:

1. When the question asks for an exact answer, you’ll need to use fractions or decimals. For example, if someone asks you how much a pizza costs and the menu only lists prices in whole dollars, you’ll need to use fractions or decimals to give an accurate answer.
2. When the question doesn’t require an exact answer, you can usually round off. For instance, if someone asks you how far it is from your house to the nearest store, you can probably just give a rough estimate in miles rather than using fractions or decimals.
3. When working with money, it’s usually best to be precise and use fractions or decimals. This way, there’s no risk of overspending or being shortchanged.
4. In general, it’s always better to err on the side of caution and be more precise rather than less precise. If you’re not sure whether a question requires an exact answer, it’s better to give one than to risk giving an inaccurate estimate.

By following these guidelines, you’ll be able to know when to give an answer in fractions or decimals. Just remember that the key is to understand the question and what level of precision is required.

What is the difference between fractions and decimals?

Fractions and decimals are both ways of representing numbers that are not whole numbers. A fraction represents a number that is a part of a whole, while a decimal represents a number that is smaller than one.

The main difference between fractions and decimals is that fractions are written as ratios, while decimals are written as division. For example, the fraction ¾ can be written as 3/4, which means that there are three parts of the whole and the number being represented is one of those three parts. The decimal 0.75 can be written as 7/10, which means that the number being represented is seven tenths of the whole.

Another difference between fractions and decimals is how they are used in mathematical operations. When adding or subtracting fractions, the denominators (the bottom number in a fraction) must be the same. However, when adding or subtracting decimals, there is no need to line up the decimal points; simply add or subtract the numbers as if they were whole numbers. For example, to add ¾ + ⅓, you would find a common denominator (in this case 12) and then add 3 + 4 to get 7/12. To add 0.75

How to convert fractions to decimals?

When you’re working with fractions, you sometimes need to convert them to decimals in order to make calculations easier. Here’s a step-by-step guide on how to do that:

1. Start by finding the fraction’s numerator (top number) and denominator (bottom number).
2. Divide the numerator by the denominator. This will give you the decimal equivalent of the fraction.
3. If your answer is a repeating decimal, you can use a bar over the digits that repeat to indicate this. For example, if you divide 1 by 3, you’ll get 0.333… which means that the 3 repeats indefinitely. So we would write this as 0.(3).
4. That’s all there is to it! With a little practice, you’ll be converting fractions to decimals in no time.

What are common denominators?

One of the most basic concepts in mathematics is that of a common denominator. A common denominator is simply a number that is a multiple of all the other numbers in a given set. In other words, it is a number that can be evenly divided by all the other numbers in the set.

The most common use for finding a common denominator is when adding or subtracting fractions with different denominators. In order to add or subtract fractions, they must first have a common denominator. Once this is found, the numerators (top numbers) can be added or subtracted as normal and then placed over the new common denominator.

For example, say we want to add 1/3 + 1/4. We can find a common denominator by finding the least common multiple of 3 and 4, which is 12. We then rewrite each fraction so that their denominators are both 12:

1/3  becomes  4/12

1/4  becomes  3/12

Now we can simply add the numerators and place them over the new common denominator:

4/12 + 3/12 = 7/12

Therefore, 1/3 + 1/4 = 7/12.

There are a few different methods that can be used to find a common denominator, but the most important thing is to remember that it must be a number that is a multiple of all the other numbers in the set. With a little practice, finding common denominators will become second nature!

How to convert decimals to fractions?

When you’re working with fractions, you sometimes need to convert a decimal to a fraction (or vice versa). Here’s how to do it:

To convert a decimal to a fraction, take the decimal and multiply it by 10, 100, 1000, etc. until you get a whole number. Then count the number of zeros in the denominator. That will be the numerator of your fraction. The denominator will be 10 with that many zeros.

For example, let’s convert 0.75 to a fraction. We multiply 0.75 by 100 to get 75:

0.75 * 100 = 75

Since there are 2 zeros in the 100 (10 squared), the final fraction is 75/100 or 3/4.

You can use this same method to convert fractions to decimals – just divide instead of multiplying!

What is a mixed number?

A mixed number is a whole number plus a fraction. For example, 3 1/2 is a mixed number. It can be written as a fraction: 7/2.

Comparing fractions and decimals?

When it comes to fractions and decimals, there are a few key things to keep in mind. For starters, fractions represent a part of a whole, while decimals represent a portion of a whole. In other words, fractions are used when we want to express how many parts of something there are, while decimals are used when we want to express how much of something there is.

Another key difference between fractions and decimals is that fractions are always written with a numerator (the number above the line) and a denominator (the number below the line), while decimals are written with just a number followed by a decimal point.

So, how do we compare fractions and decimals? Well, it all comes down to understanding what each one represents. If we want to compare two parts of a whole, then we would use fractions. However, if we want to compare two portions of a whole, then we would use decimals.

Here’s an example: Let’s say we have two pieces of pizza: one is half pepperoni and half cheese, while the other is one-third pepperoni and two-thirds cheese. If we wanted to compare the amount of pepperoni between the two pizzas, we would use fractions. In this case, the first pizza would be 1/2 pepperoni and the second pizza would be 1/3 pepperoni. As you can see, the first pizza has more pepperoni than the second.

On the other hand, if we wanted to compare the amount of cheese between the two pizzas, we would use decimals. In this case, the first pizza would be 0.5 cheese and the second pizza would be 0.67 cheese. As you can see, the second pizza has more cheese than the first.

So, when it comes to comparing fractions and decimals, it all depends on what you’re trying to compare. Just remember that fractions represent parts of a whole while decimals represent portions of a whole, and you’ll be able to make comparisons accordingly!

What are the different types of fractions?

There are three different types of fractions: proper fractions, improper fractions, and mixed numbers.

Proper fractions are those where the numerator (top number) is less than the denominator (bottom number). For example, 1/2, 2/3, and 4/5 are all proper fractions.

Improper fractions are those where the numerator is greater than or equal to the denominator. For example, 5/4, 6/5, and 15/8 are all improper fractions.

Mixed numbers are a combination of a whole number and a fraction. For example, 3 1/2, 4 2/3, and 5 3/4 are all mixed numbers.

How to add and subtract fractions?

There are many different types of fractions, but the three most common are improper fractions, mixed numbers, and decimals.

Improper fractions are when the numerator (top number) is larger than the denominator (bottom number). For example, 3/2 is an improper fraction. This type of fraction can be converted to a mixed number by adding the whole number to the numerator. So, in this case, 3/2 would become 1 1/2.

Mixed numbers are when there is both a whole number and a fraction together. For example, 1 1/2 is a mixed number. This type of fraction can be converted to an improper fraction by multiplying the denominator by the whole number and adding it to the numerator. So, in this case, 1 1/2 would become 3/2.

Decimals are another way to represent fractions. They are especially useful when working with large numbers or very small numbers that aren’t easily represented as fractions. To convert a decimal to a fraction, simply write it as a division problem using powers of ten in the denominator. For example, 0.125 can be written as 125/1000 or 1/8.

What are equivalent fractions?

An equivalent fraction is a fraction that is equal to another fraction. The two fractions have the same value, but they may look different. For example, 1/2 is an equivalent fraction to 2/4. They both represent the same amount: half of something.

To find an equivalent fraction, you can multiply or divide both the top and bottom number (the numerator and denominator) by the same number. As long as you don’t change the order of the numbers, the fractions are still equivalent.

Here’s an example:

Let’s say you have a pizza that you want to share with your friends. You cut it into 8 slices, and you give each friend 2 slices. But then you realize that 2 of your friends are vegetarian, so they can’t eat pizza! So you give them each 1 slice of bread instead.

You now have 6 slices of pizza and 2 slices of bread. You could say that this is equivalent to 3/4 + 1/8. Or you could say that this is equivalent to 9/12 + 1/24. As long as the order of the numbers stays the same, the fractions are equivalent.

Equivalent fractions are a helpful way to simplify fractions. If you can find an equivalent fraction that is easier to work with, it can make your life a lot easier!

Conclusion

We hope this blog post “How to Know When to Give an Answer in Fractions Or Decimals?” has helped clear up any confusion you may have had. If you have any further questions, feel free to reach out to us and we would be happy to help!

Today sponsors are Hutto TX Roof Repair and Infinity Charm