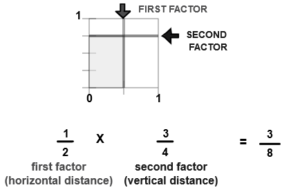
Math Lesson 4: How Many Fractions Are Greater Than One-Eighth But Less Than 15-32? In the last few questions, we asked how many fractions are larger than one-eighth and less than fifteen-third. The answer is 0.46875. There are two different ways to find the answer to this question. First, you can use a calculator to check the size of fractions. Next, you can use an app like this one to calculate the answer.
Part one of this lesson introduces the concept of fractions. Fractions are classified as greater than one, less than one, or equal to one. Part two of the lesson gives students continued practice with fractions. Students sort fractions by their relationship to one and provide examples. Part 3 focuses on more advanced questions and requires students to compare fractions with different fractions. This way, they can better understand how fractions are formed.
In the next lesson, we’ll discuss how to multiply fractions. Fractions are divided into denominators and numerators. Then, the fractions are multiplied to find a common denominator. To simplify fractions, you can divide the numerator and denominator by the greatest common factor, such as one, two, or three. The lower form is the simplest and most straightforward.
What fraction is bigger 3/32 or 1 8?
It’s a common question: which fraction is bigger, 3/32 or 1/8? The answer might not be as straightforward as you think!
To compare fractions, we need to find a common denominator. In this case, the lowest common denominator is 32. So, we can rewrite both fractions as follows:
3/32 = 9/96
1/8 = 32/256
Now that the fractions have a common denominator, we can directly compare the numerators: 9 is less than 32, so 3/32 is less than 1/8.
Of course, there’s an easier way to compare these fractions. We can simply look at the decimal equivalents:
3/32 = 0.09375
1/8 = 0.125
It’s clear that 0.125 is greater than 0.09375, so 1/8 is greater than 3/32.
So, the next time someone asks you which fraction is bigger, 3/32 or 1/8, you can confidently say that 1/8 is greater than 3/32!
How do you know which fraction is greater than less than?
When it comes to fractions, the larger the number on top, or the numerator, the greater the value of the fraction. This is because fractions represent a division of two numbers, with the numerator being the number being divided and denominator being what it’s being divided by. So, a fraction like ¾ can be seen as three out of four parts, or three divided by four. In this case, since 3 is larger than 1 (the numerator is larger), we know that ¾ is also larger than ½.
It can be helpful to think of fractions as a pie chart. If we have two pies and one has ¼ of its pie left while the other has ⅓ of its pie left, we can see that there’s more “pie” remaining in the second pie. Therefore, ⅓ is larger than ¼.
Similarly, if we have two lines and one line is twice as long as another line, then we know that the longer line is also twice as big as the shorter line – even if we don’t know how long either line actually is. So in terms of fractions, 2/5 is bigger than 1/5 because 2 is bigger than 1.
This is also why fractions with larger denominators are usually smaller than fractions with smaller denominators. For example, ¼ is less than ⅕ because 4 is larger 5, even though both fractions represent the same amount of pie (or line).
Keep in mind that there are some exceptions to this rule. If a fraction has a numerator of 0, then it will always be less than any other fraction (except for another fraction with a numerator of 0). So 0/5 is always going to be less than 3/5 or 4/7, etc. The only time when two fractions with different numerators and different denominators can have the same value is when the numerators are equal to each other and the denominators are also equal to each other – like 2/4 and 3/6. In this case, we say that the fractions are “equivalent” and they can be used interchangeably.
When it comes down to it, comparing fractions isn’t too difficult once you get the hang of it. And if you ever need a little extra help, just remember: The bigger the top number, the greater the value of the fraction.
How do I know if a fraction is greater than?
When you are comparing two fractions, the first thing you need to do is find a common denominator. Once you have found a common denominator, you can compare the numerators of the fractions. The fraction with the larger numerator is the greater fraction.
For example, let’s say we want to compare the following fractions: ¾ and 1/5
The first step is to find a common denominator. In this case, it would be 20. So we would rewrite both fractions as follows:
15/20 and 4/20
Now that we have a common denominator, we can compare the numerators of both fractions. 15 is greater than 4, so ¾ is greater than 1/5.
Comparing fractions can seem tricky at first, but if you follow these steps it will be easy!
Which number is greater in fractions?
When it comes to fractions, the answer to this question can be a bit more complicated than you might think. In order to determine which number is greater in fractions, you first need to understand what a fraction is. A fraction is simply a number that represents a part of a whole. For example, if you have a pie and cut it into eight pieces, each piece would be one-eighth of the pie.
Now that we know what fractions are, let’s talk about how to compare them. When comparing two fractions, there are three things you need to consider: the numerator (the top number), the denominator (the bottom number), and the size of the whole. Let’s look at an example:
Say we have two fractions: 1/4 and 2/9. To figure out which fraction is greater, we need to compare their numerators and denominators. In this case, the numerator for 1/4 is smaller than the numerator for 2/9. But that doesn’t necessarily mean that 2/9 is larger than 1/4 – we also need to consider the size of the whole.
To do this, we need to find a common denominator between the two fractions. The easiest way to do this is to multiply the numerator and denominator of each fraction by the same number. For our example, we’ll multiply 1/4 by 9/9 and 2/9 by 4/4. This gives us 9/36 and 8/36. Now we can compare the two fractions using their new numerators: since 8 is greater than 9, 8/36 is greater than 9/36, and therefore 2/9 is greater than 1/4.
As you can see, comparing fractions can be a bit tricky. But as long as you remember to consider the numerator, denominator, and size of the whole, you should be able to figure out which number is greater in any fraction comparison problem.
What fraction is bigger 3 4 or 4 5?
It’s a common question: which fraction is bigger, 3/4 or 4/5? The answer may not be as simple as you think.
Here’s a quick way to compare fractions: find the lowest common denominator (LCD). The LCD of 3/4 and 4/5 is 20. That means that 3/4 is equal to 15/20 and 4/5 is equal to 16/20. So, which fraction is bigger? 15/20 or 16/20?
The answer is 16/20. So, in this case, 4/5 is the larger fraction.
Keep in mind that the LCD isn’t always the smallest number that both fractions will go into. In some cases, it may be the largest number. For example, the LCD of 2/3 and 3/4 is 12. That means that 2/3 is equal to 8/12 and 3/4 is equal to 9/12. So, 8/12 is smaller than 9/12 and, in this case, 2/3 is the smaller fraction.
When you’re trying to compare fractions, the best thing to do is to find the LCD and then compare the numerators. That way, you can be sure that you’re comparing apples to apples (or, in this case, fractions to fractions).
How do I compare fractions?
Comparing fractions can be a tricky business, but there are a few methods you can use to make it a little easier. The first step is to make sure that the fractions have the same denominator – this is the number at the bottom of the fraction. Once you’ve done that, you can either line the fractions up side by side and compare them like that, or you can convert them both into decimals and compare them that way.
If you’re having trouble converting fractions into decimals, don’t worry – there’s a method for that too. To convert a fraction into a decimal, divide the numerator (the number at the top of the fraction) by the denominator (the number at the bottom). So, if we take the fraction ¾ as an example, we would divide 3 by 4 to get 0.75. Make sense?
Once you’ve got your two fractions in decimal form, it’s simply a matter of comparing which one is larger. If they’re both equal – congratulations! You’ve just successfully compared two fractions!
Comparing fractions doesn’t have to be a headache – with a little practice, you’ll be doing it like a pro in no time.
What are 4 ways to compare fractions?
When it comes to fractions, there are a few different ways that you can compare them. In this blog post, we’re going to take a look at 4 different ways that you can compare fractions.
The first way to compare fractions is by looking at the numerators. The numerator is the top number in a fraction, and it represents how many parts of the whole you have. So, if two fractions have the same numerator, then they have the same number of parts. For example, if we have 1/2 and 2/4, we can see that both fractions have the same numerator (1). This means that they both have 1 part of the whole.
The second way to compare fractions is by looking at the denominators. The denominator is the bottom number in a fraction, and it represents how many parts make up the whole. So, if two fractions have different denominators, then they have different numbers of parts making up their respective wholes. For example, if we have 1/4 and 2/8, we can see that these fractions have different denominators (4 and 8). This means that 4 parts make up one whole in the first fraction while 8 parts make up one whole in the second fraction.
The third way to compare fractions is by looking at the relationship between the numerator and denominator. If the numerator is larger than the denominator, then the fraction represents a larger number than if the numerator was smaller than the denominator. For example, 3/4 is a larger number than 1/2 because 3 is larger than 1.
The fourth and final way to compare fractions is by converting them to decimals. To do this, you simply divide the numerator by the denominator. So, if we have 1/4 and 2/8, we would get 0.25 for the first fraction and 0.50 for the second fraction. As you can see, these numbers tell us that 2/8 is actually a larger number than 1/4, even though they have different numerators and denominators.
So there you have it! These are four different ways that you can compare fractions. When it comes time to compare fractions, make sure to use one (or more) of these methods so that you can accurately find which fraction is larger or smaller!
How do you find the difference between 2 fractions?
When two fractions have the same denominator, finding the difference is simple subtraction. For example, the difference between 1/4 and 3/4 is 1/4 – 3/4, which equals -1/2.
But what happens when the denominators are different? In order to subtract two fractions with different denominators, you need to first find a common denominator. The common denominator will be the least common multiple (LCM) of the two original denominators.
To find the LCM of two numbers, start by listing out all of the factors of each number. The LCM is equal to the product of all factors that appear in both lists:
Factors of 4: 1, 2, 4
Factors of 6: 1, 2, 3, 6
The LCM of 4 and 6 is 12 because it’s the smallest number that has both 1 and 2 as factors.
So now that we know how to find a common denominator when adding or subtracting fractions with different denominators, let’s go back to our original problem: 1/4 – 3/4. We can rewrite this as follows:
(1/4) x (3/3) – (3/4) x (3/3)
Now we have two fractions with a common denominator of 3. This means we can simply subtract the numerators to find the answer:
(1/4) x (3/3) – (3/4) x (3/3)
= 1/12 – 9/12
= -8/12
= -2/3
What fraction is bigger 2/3 or 3 4?
There is a common misconception that the fraction 3/4 is bigger than 2/3. In reality, it depends on the context in which you are looking at these fractions. If you are working with whole numbers, then 3/4 is indeed larger than 2/3. However, if you are working with decimals, 2/3 is actually the larger fraction.
To understand why this is, let’s look at an example. Say we have two pies, and we want to divide them up into equal parts. One pie has 8 slices, and the other has 12 slices. If we use 8ths as our denominator, then we get that each slice of the first pie is 1/8th of the pie, and each slice of the second pie is 1/12th of the pie. This means that 3 slices of the first pie would be equivalent to 2 slices of the second pie (1/8th * 3 = 1/12th * 2).
However, if we use 10ths as our denominator instead, then we get that each slice of the first pie is still 1/8th of thepie , but each slice ofthe second pies now equals 1 /10 thof t hepie . This means that 3 slices of the first pie would now be equivalent to 1.5 slices of the second pie (1/8th * 3 = 1/10th * 1.5). Therefore, in this context, 2/3 is actually the larger fraction.
Keep this in mind next time you are trying to compare fractions!
Which one is bigger 4 7 or 2 3?
In mathematics, the concept of order is crucial. It helps us to understand and compare numbers in a variety of ways. For example, we can ask: which one is bigger, 4 or 7? The answer is obvious – 7 is bigger than 4. But what about 2 and 3? Which one is bigger in this case?
The answer might not be so obvious now, but it turns out that 3 is indeed bigger than 2. To see why, let’s look at a specific example. Imagine we have two bags of sweets, one with 4 sweets and one with 7 sweets. Now imagine we have another two bags of sweets, each with 2 sweets inside. So which bag has more sweets overall?
The answer is the first bag – the one with 4 sweets inside. Even though there are fewer individual sweets in this bag, when we compare the total number of sweets across all four bags, the first bag comes out on top (4 + 2 > 3 + 7).
This same principle can be applied to any other numbers too. So next time you’re wondering whether 4 or 7 is bigger, or whether 2 or 3 is bigger, remember to think about how many items are in each group before making your decision!
Which fraction is bigger 4 5 or 2 3?
There are a few different ways that we can compare fractions. In this case, we are looking at which fraction is bigger when both fractions have the same denominator. When the denominator is the same, we compare the numerators. The fraction with the bigger numerator is the larger fraction. In this case, 4/5 is larger than 2/3 because 4 is greater than 2.
We can also compare fractions by converting them to decimals. When we convert fractions to decimals, we divide the numerator by the denominator. So, 4/5 becomes 0.8 and 2/3 becomes 0.666666…. As you can see, 0.8 is larger than 0.666666…, so 4/5 is also larger than 2/3 in decimal form!
Finally, another way to compare fractions is by using a visual representation like a number line or a hundred chart. If we put 4/5 on a number line or hundred chart, it would fall between 0 and 1 because it’s equal to 0.80 (4 divided by 5). Where would 2/3 go? It would also fall between 0 and 1 because it’s equal to 0.666666…. So, on a number line or hundred chart, 4/5 is also larger than 2/3.
No matter which way you compare them, the fraction 4/5 is always going to be larger than the fraction 2/3!
Which fraction is bigger 1/4 or 2 3?
When it comes to fractions, the answer to this question may not be as simple as you think. In order to determine which fraction is bigger, we need to compare the numerators and denominators of each fraction. In this case, we are comparing 1/4 and 2/3.
The first thing we notice is that the denominators are different. When fractions have different denominators, we need to find a common denominator before we can compare them. The easiest way to do this is by finding the least common multiple (LCM) of the two denominators. In this case, the LCM of 4 and 3 is 12.
Once we have our common denominator, we can rewrite each fraction using it: 1/4 becomes 6/12 and 2/3 becomes 8/12. Now that both fractions have the same denominator, it’s easy to see that 8/12 is larger than 6/12 (and therefore 2/3 is larger than 1/4).
Of course, there’s another way to approach this problem without having to find a common denominator. If you look closely at the two fractions, you’ll notice that 2/3 is actually 1 1/3 – in other words, it’s one whole plus one third. 1/4, on the other hand, is just one quarter (or two eighths). So when we compare 1 1/3 to 1/4, it’s clear that 1 1/3 is larger.
So there you have it – the answer to our question is 2/3 (or 1 1/3)!
Conclusion
We hope this blog post “Math Lesson 4: How Many Fractions Are Greater Than One-Eighth But Less Than 15-32?” has helped clear up any confusion you may have had. If you have any further questions, feel free to reach out to us and we would be happy to help!
Hey, check out: What is One-Third of a Quarter?
Today sponsors are Localhandymantulsa.com , sprinklerrepairlongisland.com , Mailboxrepairtulsa.com , Chestercountytowingservices.com and Huttotxroofrepair.com. Always providing the best services in town.