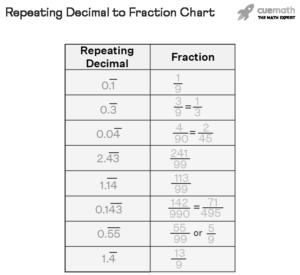
How to Convert Repeating Decimals Into Fractions? If a number has two digits that repeat, it is called a “repeating decimal.” In a basic repeating decimal, one digit repeats and the rest does not, the formula for converting it into a fraction is as follows: 0.4444 = 0.583-. However, in a mixed repeating decimal, the repeating number does not repeat until the tenth place.
To convert a repeating decimal to a fraction, multiply the number by a power of ten to move the decimal point to the right. Then, find another equation with the same decimal number, and subtract the smaller equation from the larger one to get a fraction. Once the repeating digit is removed, the number is converted to a fraction. Once you have the digits you want, simply multiply them by the remainder of the original fraction, which will give you a fraction.
To convert a repeating decimal to a fraction, you must know the meaning of the “repeating” digit. This is an indicator that a number is a repeating one. In some cases, the number may be marked with a dotted line over the repeating digits. For example, 3.7777 is a repeating decimal, but it is written as 3.7. A recurring decimal can be converted into a fraction by solving an equation.
You may wonder how to convert a repeating decimal into a fraction. The answer to this question is in the number’s terminating decimal. The first digit represents the tenth, the next digit is the hundredth, and the next digit is the thousandth. For example, 0.5 means a fifth. For the same reasoning, 0.3125 is a fraction equal to three and a half hundred tenths. In this way, the fraction can be simplified by making it a mixed fraction.
A fraction containing a recurring decimal with an even length has a “cyclic” structure. The ellipsis introduces uncertainty about the number of digits that will repeat. For example, a recurring decimal in the form of a fraction with a coprime of 10 will have a cyclic structure. In this case, the repeated digit is a factor of p – 1.
You must first determine the initial transient. Remember that the initial transient might contain some zeros. For example, 75/100 is a recurring fraction, and 3/4 of a century is a common one. If the initial transient has six digits, then the repeating block is a fraction of pk ql. Then, the repeating block is a three-digit block. Further, a repeating block of z equals four/333.
How do you change a repeating decimal into a fraction?
A repeating decimal is a number that has a digit or digits that repeat endlessly. In order to change a repeating decimal into a fraction, you need to identify the digits that are repeating. Once you have identified the repeats, place them over a 9 and reduce. For example:
0.3333… would be 3/9 because the digit 3 repeats endlessly
0.1666… would be 1/6 because the digit 6 repeats endlessly
0.142857142857142857… would be 1/7 because the digit 7 repeats endlessly
0.125 would be 1/8 because the digit 2 repeats endlessly
If a decimal does not repeat, it can be changed into a fraction by counting the number of digits after the decimal point and placing that number over a power of 10. For example:
0.5 would be 5/10 because there is one digit after the decimal point (the 5). 10 to the power of 1 is 10, so we place 5 over 10
0.25 would be 25/100 because there are two digits after the decimal point (the 2 and the 5). 100 to the power of 2 is 100, so we place 25 over 100.
Can a repeating decimal be written as a fraction?
What is 0.22 repeating as a fraction?
When it comes to fractions, 0.22 repeating can be a bit of a tricky one. So, what exactly is 0.22 repeating as a fraction?
Well, to understand 0.22 repeating as a fraction, we need to take a look at what happens when we try to divide 22 by 9. When we do this, we get 2 with a remainder of 4. This means that the decimal equivalent of 0.22 repeating is actually 22/9.
Now, when we try and convert this into a fraction, we run into a bit of trouble because 9 goes into 22 twice with a remainder of 4. This means that our fraction ends up being 2 4/9 which can be simplified to 2 1/3.
So there you have it! 0.22 repeating as a fraction is actually 2 1/3.
What is 0.33333 repeating as a fraction?
What is 0.166 repeating as a fraction?
If you’re like most people, you probably think of fractions as numbers like ¼ or ½. But there are actually an infinite number of fractions! In fact, any number that can be written as a decimal can also be written as a fraction. For example, did you know that 0.166 repeating is equal to 1/6?
To understand why, let’s take a closer look at what it means for a decimal to repeat. When we write a decimal like 0.166, the “6” at the end just means that the number keeps going on forever. So really, we could write it like this: 0.166…
Now let’s think about what would happen if we tried to divide 1 by 6. We would get this:
1/6 = 0.166666…
Do you see the pattern? The “6” repeats infinitely! So when we say that 0.166 repeating is equal to 1/6, all we’re saying is that these two numbers are equivalent.
Of course, you can use this same method to figure out what any repeating decimal is equal to as a fraction. Just divide 1 by the number that the decimal repeats. For example, 0.25 repeating is equal to 1/4, and 0.33 repeating is equal to 1/3.
So the next time you see a repeating decimal, don’t be afraid to turn it into a fraction!
How do you write 6.66 as a fraction?
When you see a number like 6.66, it can be tempting to write it as 666/100. However, this would be incorrect. The number 6.66 is actually equal to 2/3, or 66/100.
To understand why, let’s take a look at what those numbers mean. The number 6.66 is a repeating decimal, which means that the 3 repeats endlessly after the decimal point. This can be written as 3∞.
The number 666 is also a repeating decimal, but in a different way. It has a 6 repeating infinitely, but it also has other numbers before and after the decimal point. This can be written as 6666… ∞
Now let’s look at what 2/3 and 66/100 mean:
2/3 means that for every 3 parts of something, there are 2 of them
66/100 means that for every 100 parts of something, there are 66 of them
In both cases, we’re talking about division – specifically dividing by 3 or 100 respectively.
So when we want to write 6.66 as a fraction, we need to find an equivalent fraction where the denominator (the bottom number) is 3 or 100. 66/100 is already in this form, so we can just leave it as is.
2/3 is also an equivalent fraction, but we need to make a few changes first. Remember, 2/3 means that for every 3 parts of something, there are 2 of them. In other words, 2 divided by 3 equals 0.666…
We can use this information to write 2/3 as a decimal:
2/3 = 0.666…
From there, it’s just a matter of converting 0.666… into 66/100. We do this by multiplying both the numerator and denominator by 15:
2/3 = (2*15)/(3*15) = 30/45 = 66/100
And there you have it! 6.66 written as a fraction is either 2/3 or 66/100.
How do you write 66.6% as a fraction?
When you see a decimal like 66.6%, it’s easy to assume that the percentage sign means “divide by 100,” but that’s not always the case. In this instance, the percent sign actually means “out of 100,” so 66.6% is equal to 66.6 out of 100, or 2/3.
You can convert a decimal to a fraction by moving the decimal point two places to the left and dropping the percent sign:
66.6% = 0.666 → 0.666 → 2/3
How do you write 16.66 as a fraction?
When you see a decimal like 16.66, it can be hard to know what to do with it. After all, how can you have a fraction with a decimal in the middle of it? But there’s a simple way to convert any decimal into a fraction.
Here’s how you do it:
- Find the place value of the number after the decimal point. In 16.66, that number is 66.
- Move the decimal point up so that it’s in front of the 66, and put a 1 in front of the 6 (because when you move the decimal point, all other numbers get moved over one place value as well). So 16.66 becomes 166.6
- Now that there’s no decimal point, you can treat this like any other whole number fraction and simplify as much as possible. In this case, 166 is divisible by 2 twice (83 divided by 2 is 41 1/2, which divided by 2 again is 20 3/4), so 166 divided by 2 is 83. Then 83 divided by 2 again is 41 1/2, or just 41 if we’re not looking for fractions with halves or fourths in them (we could also divide 83 by 4 to get 20 3/4, which is the same answer).
- So 16.66 simplified as a fraction is 41/2, or 20 3/4.
What is .66666 repeating as a fraction?
What is 1.333 repeating as a fraction?
We all know what fractions are – they are numbers that represent a part of a whole. But what exactly is 1.333 repeating as a fraction?
This number is actually what’s called a recurring decimal, which means that the decimal point keeps coming back after every three digits. In other words, the 3s keep repeating indefinitely. So how do we turn this into a fraction?
Well, we can actually break this down quite easily. The first thing to note is that the number before the decimal point (1) stays the same, no matter how many times the 3s repeat. So our fraction will always have 1 as its numerator (top number).
As for the denominator (bottom number), we just need to count how many digits there are after the decimal point – in this case, it’s three. So our final fraction would be 1/3 repeated, or 1/33 if you want to be more specific.
So there you have it! The next time you come across a recurring decimal, you’ll know exactly how to turn it into a fraction.
How do you turn 0.667 into a fraction?
When you want to turn a decimal like 0.667 into a fraction, there is a simple process you can follow to make it happen. All you need to do is multiply the decimal by 100, and then put that number over 100. So, for 0.667, you would multiply it by 100 to get 66.7. Then, you would put 66.7 over 100 as your final answer. You could also simplify this fraction by dividing both the top and bottom by 10, which would give you 6 67/100 as the final answer.
Decimals are a sometimes tricky concept for students first encountering them in their math studies. But with a little practice, they can be easy to work with – especially when it comes to turning them into fractions. The process is really quite straightforward: simply multiply the decimal by 100, and then put that number over 100.
For example, let’s say you want to turn 0.667 into a fraction. To do so, you first multiply 0.667 by 100 to get 66.7. Then, you put 66.7 over 100 as your final answer. You could also simplify this fraction by dividing both the top and bottom by 10, which would give you 6 67/100 as the final answer.
The key is to remember that when you’re working with decimals, moving the decimal point to the right is like multiplying by 10 (or 100, or 1000, and so on). So if you want to turn a decimal into a fraction, just think about where the decimal point needs to go in order for the number to be turned into an equivalent fraction – and then make that move!
What is 24.41 as a fraction?
How do you write 0.35% into a fraction?
How do you write 0.11111 as a fraction?
When we see a decimal like 0.11111, we can think of it as a fraction. The number to the left of the decimal point is the whole number, and the number to the right is the numerator (or top number) of the fraction. In this case, we have 1 whole and 4/9ths.
We can also use place value to help us write this as a fraction. The 5 in 0.11111 is in the thousandths place, which means it has a value of 5/1000, or 1/200. So far, we have 1 + 1/200.
The next digit is a 1, which is in the hundredths place. This has a value of 1/100, or 1/10. So our fraction so far becomes 1 + 1/10 + 1/200.
The next digit is another 1, which has a value of 1/10. So our fraction becomes 1 + 2/10 + 1/200.
The final digit is a 1, which has a value of 1/10. So our fraction becomes 1 + 3/10 + 1/200.
When we put it all together, we have the fraction 1 3/10 + 1/200.
What is 0.555 as a fraction?
0.555 can be written as a fraction in a few different ways. The simplest way would be to multiply both the numerator and denominator by 1000, which would give you the fraction 555/1000. However, this is not the most simplified form of the fraction.
To simplify this fraction even further, we can look at it as a mixed number. In other words, we can write 0.555 as the whole number 0 plus the fraction 555/1000. This mixed number can then be simplified by dividing the numerator (555) by the denominator (1000), which gives us the answer 5/9 in its simplest form.
We could also look at this problem a different way and convert 0.555 into an improper fraction first. To do this, we simply take the decimal point out of 0.555 and move it two spaces to the right, giving us 555/1000 as our improper fraction. We can then simplify this just like we did before by dividing 555 by 1000, which still gives us 5/9 in its simplest form.
So, in conclusion, there are a few different ways that we can write 0.555 as a fraction. The simplest way is to multiply both the numerator and denominator by 1000, which gives us 555/1000. However, this fraction can be further simplified by looking at it as a mixed number or an improper fraction and dividing the numerator by the denominator, which gives us the answer 5/9 in its simplest form.
Conclusion
We hope this blog post “How to Convert Repeating Decimals Into Fractions” has helped clear up any confusion you may have had. If you have any further questions, feel free to reach out to us and we would be happy to help!
Hey, check out: What Rational Number is Between 3/4 and 7/8 in Decimal Form?
Today sponsors are Localhandymantulsa.com , sprinklerrepairlongisland.com , Mailboxrepairtulsa.com , Chestercountytowingservices.com and Huttotxroofrepair.com. Always providing the best services in town.