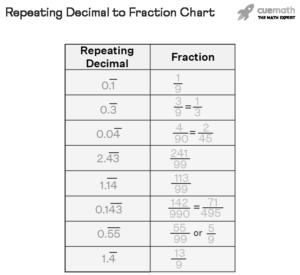
If a fraction contains a repeating decimal, you can use the following steps to figure out which fraction is a repeating decimal: First, multiply the number by a power of 10 and look for the ending digit. If the number has two and five factors, the decimal point is placed to the right of the repeating digit. Next, find the fraction’s smaller equivalent and subtract it from the larger fraction.
Likewise, a fraction with a repeating decimal will have multiple remaining digits. These digits will never exceed the number of digits in the denominator. The repeating digits will be referred to as k. As k is equal to d – 1, you can easily find the repeating decimal representation of a fraction by looking at its digits.
Once you know how to recognize a repeating decimal, you can test your conjecture with more examples. For example, Jose wants to give three of his friends 10 chocolate bars. You should see that the decimal expansion repeats when you divide 10 by three. Then, divide the remainder by nine. And so on. You can also identify a repeating decimal by using the technique of dividing a number by 3 and a fraction by eight.
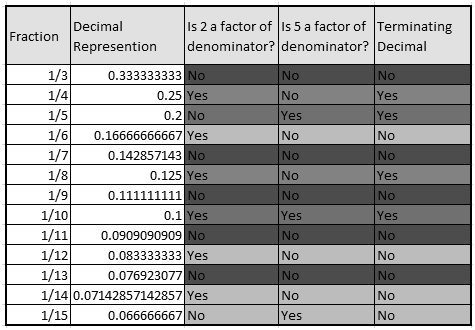
If you are looking at a number with a repeating decimal, you might be wondering whether it is a repeated one. It is important to note that the same decimal number appears more than once. This is a common mistake that you need to avoid. By knowing the repeating decimal, you will avoid a lot of mistakes in calculations. So, if you are confused, you can practice the problem and solve it with ease.
Another way to find out whether a fraction is a repeated decimal is by checking the length of the repeated decimal. All fractions with coprime to ten always have a repeating decimal. If the repeating decimal is 1/p, then it is a repeated decimal. The repeating decimal 1/p has a length of one order of 10 modulo p, and for a prime r p, it is a factor of p – 1.
Another way to tell if a fraction has a repeated decimal is to consider its representation. In some countries, a repeating decimal is an irrational number, meaning that it is not a ratio of two integers. For example, p is irrational, but it is also a square with length one. It is also called a repeating decimal.
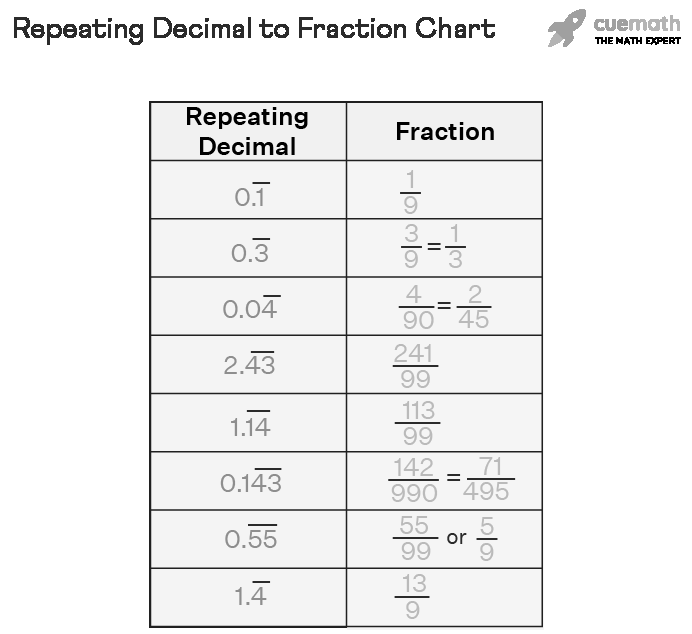
What is the rule for repeating decimals?
Repeating decimals are decimal numbers that have a digit or digits that repeat endlessly. The rules for repeating decimals are as follows:
To convert a fraction with a denominator of 10 or 100, simply divide the numerator by the denominator. The answer will be a repeating decimal if the fraction is not equal to zero.
To convert a fraction with a denominator that is not 10 or 100, first divide the numerator by the denominator. This will give a non-repeating decimal. Next, multiply the denominator by itself until you get a number that is 10 or 100 times the original denominator. Divide the original numerator by this new number. The answer will be a repeating decimal.
How do you find if a fraction is terminating or repeating?
When it comes to fractions, there are two different types: terminating and repeating. So, how can you tell which type you have? Here are a few things to look for:
First, take a look at the denominator. If it’s a power of 2 or a power of 5, then the fraction is likely to be terminating. This is because these numbers can be easily divided into smaller pieces, so the fraction will eventually come to an end.
Another way to tell if a fraction is terminating is to look at the numerator. If it’s a multiple of the denominator, then the fraction will definitely terminate. For example, if the numerator is 6 and the denominator is 3, then the fraction will end after two steps: 6/3 = 2.
However, if the numerator is not a multiple of the denominator, then the fraction might repeat. For example, if the numerator is 3 and the denominator is 2, then the fraction will repeat indefinitely: 3/2 = 1.5, 1.5/2 = 0.75, 0.75/2 = 0.375, and so on.
In general, if the denominator is a prime number, then the fraction is more likely to repeat. This is because there’s no easy way to divide a prime number into smaller pieces. So, if you’re not sure whether a fraction is terminating or repeating, you can always try dividing the denominator by a few different prime numbers to see if it evenly divides.
Finally, keep in mind that some fractions can do both! For example, 1/3 will repeat forever: 1/3 = 0.333, 0.333/3 = 0.111, and so on. But if you multiply the numerator and denominator by 3, you’ll get a terminating fraction: 3/9 = 0.333, 0.333/9 = 0.037, and so on.
So, those are a few ways to tell if a fraction is terminating or repeating. In general, fractions with power denominators or multiple numerators are more likely to terminate, while fractions with prime denominators are more likely to repeat. But there are always exceptions, so it’s always best to try a few different methods to be sure.
How do you know if a decimal expansion is repeating?
If a decimal expansion is repeating, that means that the digits after the decimal point are repeating in a pattern. For example, the decimal expansion of 1/3 is 0.3333…, which is repeating the digit 3.
To determine if a decimal expansion is repeating, you can look for a patterns in the digits. If the digits after the decimal point repeat in a regular pattern, then the decimal expansion is repeating.
Another method is to divide the number by 9. If the remainder is 1, 4, 7, or 8, then the decimal expansion is repeating. This is because those remainders can only occur if the digits after the decimal point are repeating in a pattern.
For example, let’s look at the decimal expansion of 1/11. 1/11 = 0.090909… The digits after the decimal point repeat in a pattern, so the decimal expansion is repeating.
Now let’s look at the decimal expansion of 1/13. 1/13 = 0.076923… The digits after the decimal point do not repeat in a pattern, so the decimal expansion is not repeating.
To sum up, there are two main ways to determine if a decimal expansion is repeating: look for a pattern in the digits, or divide the number by 9 and check the remainder.
What do repeating decimals look like?
When a number has a decimal point and the digits after the decimal point keep repeating, it is called a repeating decimal. For example, the number 1/3 can be written as a repeating decimal: 0.3333… The three digits after the decimal point keep repeating, so this is a repeating decimal.
Some fractions can be written as non-repeating decimals. For example, the fraction 1/2 can be written as the decimal 0.5. The decimal point doesn’t repeat, so this is a non-repeating decimal.
You can usually tell if a decimal is repeating just by looking at it. If you see a decimal with a bunch of zeros after the decimal point, and then a number other than zero, the decimal is probably repeating. For example, 0.0012121212… is a repeating decimal. The zeros after the decimal point keep repeating, and then the number 1 repeats.
If you’re not sure if a decimal is repeating, you can divide the number by 9. If the result is a repeating decimal, then the original decimal is also repeating. For example, if you divide 0.3333… by 9, you get 0.111111111… which is a repeating decimal. So 0.3333… is also a repeating decimal.
You can also use long division to figure out if a decimal is repeating. For example, if you divide 1 by 3 using long division, you get the following result:
1) 3 goes into 1 0 times, so write 0 above the 1.
2) 3 goes into 10 3 times, so write 3 above the 0.
3) Subtract 3 from 10 to get 7, and write 7 below the 3.
4) 3 goes into 7 2 times, so write 2 above the 7.
5) Subtract 6 (2 times 3) from 7 to get 1, and write 1 below the 2.
6) 3 goes into 1 0 times, so write 0 above the 1.
7) Subtract 0 from 1 to get 1, and write 1 below the 0.
The numbers in bold are the digits that repeat. So 1/3 can be written as the repeating decimal 0.333…
Is 9.373 a repeating decimal?
What is 3.333 repeating as a fraction?
What is 0.33333 repeating as a fraction?
When expressed as a fraction, 0.33333 repeating is equal to 1/3. This is because the decimal 0.33333 repeating represents a fraction where the numerator is equal to 1 and the denominator is equal to 3.
To convert 0.33333 repeating into a fraction, we can use long division. We divide 1 by 3 and write down the quotient, which is 0.3333. We then bring down the next digit after the decimal point, which is 3, and divide it by 3. The quotient is 1, so we write down a 1 over the division symbol. We then bring down the next digit, which is another 3, and divide it by 3. The quotient is again 1, so we write down another 1 over the division symbol. We continue in this way, always dividing the next digit by 3 and writing down the quotient, until we reach the end of the decimal 0.33333 repeating. At this point, we have written down the fraction 1/3, which is equal to 0.33333 repeating.
Conclusion
We hope this blog post “Do Cabinet Hinges Hold Well in 23/32′ Plywood?” has helped clear up any confusion you may have had. If you have any further questions, feel free to reach out to us and we would be happy to help!
Hey check out: What Percent of Five and Eight is Eight?
Today sponsors are Lifeafter20 and Sprinkler Repair Long Island
Also check out Infinity Charm