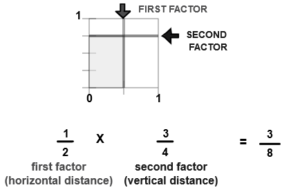
How do you find the difference between two fractions? The traditional way is to multiply the fractions together until they become smaller than each other. However, this method is not always effective. If the fractions are too large, you can reduce them to the lowest terms. If they are smaller than 40, you can divide the numerator by the denominator. Once you have the two fractions, you can find the difference between them.
To determine which fraction is greater or smaller, you first compare the numerators. When comparing fractions, look for a common denominator and compare the numerators. You can then find which fraction has a larger numerator. If the numerators are equal, you can use the same technique to compare them. This will also help you answer questions about discounts and other numerical comparisons.
First, you must determine which fractions have the lowest common denominator. Once you have the common denominator, you can add or subtract fractions. If the numerators of the two fractions are similar, then they must be added or subtracted. For example, if a fraction has a denominator of four, but has a denominator of two, you can divide it by four.
A shortcut that works well with smaller fractions is to increase the terms of the fraction. If you can multiply the denominator of a fraction by its larger numerator, you can use the cross-multiplication method. This method will yield large results, but does not require you to reduce the fractions to their lowest terms. But if you’re looking for a shortcut, this method will save you time.
If your answer is not an even number, you can use trial-and-error. You can use the LCM method to determine the numerator of a fraction. You can also divide the numerator with the denominator. Then, you’ll get the difference between the two fractions. A solved example is given below. So, if you have trouble with fractions, try this simple method to solve the problem. It will help you make calculations much easier.
Similarly, if your answer is an odd number, try to divide the fraction by the numerator. This way, you’ll get a fraction that is exactly half of the other. It is also known as the least common denominator. This method is also used to factor a large fraction. However, you should know the denominator first. Once you know the numerator, you can use Long Division with Remainders.
The difference between two numbers is called the percentage difference. The percentage difference between two numbers is the difference between the old value and the new value. Divide the new value by the old one. Negative percentage difference ignores the minus sign, while a positive percentage difference means that there’s an increase in the value. For instance, a tower that’s 30 feet tall is now 50 feet tall. This means that the height has increased by 41%.
How do you find the difference between subtracting fractions?
When subtracting fractions, you need to find a common denominator between the two fractions in order to compare them. The easiest way to do this is to find the lowest common multiple between the two denominators. Once you have the LCM, you can change both fractions so that they have that as their denominator. Then, you can simply subtract the numerators and write your answer as a fraction with the LCM as the denominator.
For example, if we want to subtract 1/4 from 3/8, we first need to find the LCM of 4 and 8. The LCM of 4 and 8 is 8. So we rewrite 1/4 as 2/8 (we multiply the numerator by 2 since 2*4=8) and 3/8 stays the same since it already has a denominator of 8. Now that both fractions have an 8 as their denominator, we can simply subtract the numerators which give us 3/8-2/8=1/8.
How do you find the sum and difference of two fractions?
Adding and subtracting fractions can be a tricky concept for many students to grasp. There are a few different methods that can be used to find the sum or difference of two fractions.
One way to find the sum or difference of two fractions is to convert both fractions to equivalent forms with the same denominator. This can be done by finding a common multiple of the two denominators, and then multiplying each fraction by an appropriate number so that both denominators are equal to this common multiple. Once the fractions are in equivalent forms, they can simply be added or subtracted like regular whole numbers.
Another method that can be used is called the ladder method. To use this method, you line up the two fractions side by side, with the larger fraction on top and the smaller fraction on bottom. You then find a number that you can multiply to both the top and bottom of each fraction so that they both have whole number answers (without changing their relative sizes). Once you have found this number, you write it above each fraction as follows:
4 3
——— ———
6 9
After writing out each fraction in this manner, you simply add or subtract across as if they were regular whole numbers, starting with the leftmost column and working your way to the right.
Both of these methods can be used to find the sum or difference of two fractions. Try out both methods to see which one works better for you!
How do you compare two fractions quickly?
Comparing fractions can be a tricky business, especially when the denominators are different. However, there are a few tricks that can make it a lot easier.
One way to compare two fractions is to find a common denominator between them. This will allow you to directly compare the numerators of the fractions, and whichever one has the larger number is the greater fraction. For example, if you’re trying to compare 1/4 and 2/9, you can find a common denominator of 36:
1/4 = 9/36
2/9 = 4/36
As you can see, 2/9 is actually the larger fraction here.
Another way to quickly compare fractions is by converting them both into decimals. To do this, simply divide the numerator by the denominator. The resulting decimal will tell you which fraction is larger. For example, let’s say you’re trying to compare 3/5 and 4/7:
3/5 = 0.6 (this is larger)
4/7 = 0.57142857142857 (this is smaller)
As you can see, in this instance, 3/5 is the larger fraction.
So next time you’re stuck trying to compare fractions, remember these two tricks! With a little practice, you’ll be comparing fractions like a pro in no time.
How do you compare two fractions with different denominators?
Comparing fractions with different denominators can be a bit tricky, but there are a few methods that can make it easier. Perhaps the simplest way to compare two fractions is to find a common denominator between them. For example, if you’re comparing 1/4 and 1/6, you can find a common denominator of 12:
1/4 = 3/12
1/6 = 2/12
Since 3 is greater than 2, you know that 1/4 is greater than 1/6.
Another method for comparing fractions with different denominators is to convert one or both fractions into equivalent fractions with the same denominator. For example, if you’re comparing 2/5 and 3/7, you could convert 2/5 to 6/15:
2/5 = 6/15
3/7 ≈ 10/15 (You can estimate by finding what 3/7 would be if it had a denominator of 15)
10 is greater than 6, so 3/7 is greater than 2/5.
You can also use a number line to compare fractions. Let’s say you’re comparing 1/3 and 2/5. You would first find a common denominator between the two fractions, which in this case is 15:
1/3 = 5/15
2/5 = 6/15
Then, you would plot these points on a number line:
When comparing fractions What are the best methods?
When it comes to fractions, there are a few different ways to compare them. The most common way is to find the lowest common denominator (LCD) and then compare the numerators. For example, if you’re comparing 1/4 and 1/6, you would find the LCD of 4 and 6, which is 12. Then you would compare 1/12 and 1/12, which are equal.
Another way to compare fractions is by using a fraction strip or number line. This can be helpful if one of the fractions is much larger or smaller than the other. For example, if you’re comparing 1/4 and 2/9, you would put these numbers on a number line:
1 2 3 4 5 6 7 8 9
|___|___|___|___|___|___|___|
|_______|
You can see that 2/9 is closer to 0 than 1/4, so it’s smaller.
The last method we’ll mention is converting fractions to decimals. You can do this by dividing the numerator by the denominator. So 1/4 would be 0.25, and 2/9 would be 0.22. Again, you can see that 2/9 is smaller than 1/4.
There are a few different ways to compare fractions, but these are some of the most common and most effective methods. Try out a few and see which one works best for you!
How do you teach compare fractions with different numerators and denominators?
When you’re teaching fractions, sometimes the hardest part can be getting students to understand how to compare fractions with different numerators and denominators. Here are a few tips to help make things a little easier for both you and your students.
One of the first things you should do is review what a fraction actually is. A fraction is a number that represents part of a whole. The numerator (top number) represents how many parts of the whole you have, while the denominator (bottom number) tells how many parts the whole is divided into. So, for example, if you have two thirds of a pie, your fraction would be 2/3. It’s important for students to understand that fractions are not just numbers written with slashes through them – they represent real division of objects or quantities.
Once your students have a good understanding of what fractions are and how they work, it’s time to start comparing them. There are a few different ways to compare fractions, but one of the simplest is by using a visual representation like a number line or bar diagram.
Let’s say we’re comparing the fractions 1/4 and 2/9. To start, we would draw out our visual representation like so:
1__2__3__4
| | |
1/4_______________|_____|_____|
| | |
1__2__3__4__5__6__7__8__9
| | | | |
2/9_______________|_____|_____|_____|_____|
Now, we can start to compare the two fractions. The first thing we notice is that 1/4 is less than 2/9 because it falls to the left on our number line. We can also see that 1/4 is larger than 1/9 (which would fall somewhere between 0 and 1 on our number line), and smaller than 2/9.
Another way to compare fractions is by finding a common denominator. This means changing both fractions so that they have the same denominator, which in turn makes them easier to compare. For our example, let’s say we want to find a common denominator for 1/4 and 2/9. The easiest way to do this is by finding the least common multiple of 4 and 9, which is 36. Once we have our new denominators, our fractions become:
1/4 = 9/36 and 2/9 = 4/36
We can see that 9/36 is larger than 4/36, so we know that 1/4 is larger than 2/9. However, if we had started with the fractions 3/4 and 2/9, we would have ended up with 36/36 and 4/36, which are both equal to 1. So in this case, it wouldn’t matter what the numerators were – the fractions would still be equal.
Comparing fractions can be a difficult concept for students to grasp, but with some review and practice it can become much easier. Using visual aids like number lines or bar diagrams can help students to see the relationships between different fractions, while finding a common denominator is a helpful way to compare fractions with different numerators.
How do you explain comparing fractions to children?
Comparing fractions can be a tricky concept for children to grasp. After all, if two parts of a whole are different sizes, how can they be equal?
Here’s a tip: start by having your child draw a picture of two fractional pieces. For example, if you’re comparing 1/4 and 1/2, have them draw a picture of a pizza cut into four pieces and another pizza cut into two pieces. Then, ask them which pizza has more ‘pizza-ness’. Of course, the answer is that they both have the same amount – it’s just that one is divided into more pieces.
From there, you can move on to explaining that when we compare fractions, we’re really just looking at how many ‘pieces’ each fraction has. So in the above example, 1/4 has one piece (out of four), while 1/2 has two pieces (out of four). Therefore, even though 1/4 looks like it’s less than 1/2, we know that it’s actually equal to 1/2 because they both have the same amount of ‘pizza-ness’, just divided up differently.
Hopefully this makes sense! If not, there are plenty of other resources out there that can help explain this concept in different ways. The important thing is to keep it visual and concrete for young learners.
How do you compare fractions 4th grade?
When it comes to fractions, there are a lot of different ways to compare them. In fourth grade, students typically learn to compare fractions by looking at the numerators and denominators. The numerator is the top number in a fraction, and the denominator is the bottom number.
To compare fractions with different numerators, you can look at the denominators to see which one is larger. For example, if you’re comparing 2/5 and 1/4, you would know that 2/5 is larger because the denominator (5) is larger than 1.
To compare fractions with different denominators, you can either find a common denominator or convert both fractions into decimals. For example, if you’re comparing 3/4 and 5/6, you could find a common denominator of 12 and then compare 3/12 and 5/12 (which would be equivalent to 0.25 and 0.42). Or, you could convert both fractions into decimals by dividing the numerator by the denominator: 3 divided by 4 equals 0.75, while 5 divided by 6 equals 0.83. This means that 3/4 is larger than 5/6.
There are other ways to compare fractions as well, but these are some of the most common methods. By understanding how to compare fractions, fourth graders will be able to better understand concepts like equivalent fractions and simplifying fractions.
How do you know which fraction is greater than less than?
Comparing fractions can be a tricky business, especially when the fractions have different denominators. There is a simple way to compare any two fractions, however, whether they have the same denominator or not. To compare fractions, simply divide the numerator of each fraction by its corresponding denominator. Whichever fraction has the greater resulting decimal is the greater of the two fractions.
For example: let’s compare 1/4 and 2/9
1/4 = .25 and 2/9 = .22
Since .25 is greater than .22, 1/4 is greater than 2/9
Or let’s compare 5/6 and 3/4
5/6 = .83 and 3/4= .75
Since .83 is greater than .75, 5/6 is greater than 3/4
Keep in mind, however, that this method of comparison only works with fractions that have different denominators. If you are trying to compare two fractions with the same denominator, simply compare the numerators of the fractions. Whichever fraction has the greater numerator is the greater of the two fractions.
For example: let’s compare 3/4 and 5/4
3/4 = .75 and 5/4= 1.25
Since 1.25 is greater than .75, 5/4 is greater than 3/4
As you can see,Comparing fractions is a breeze once you know the simple steps to take. So the next time you’re stuck trying to figure out which fraction is greater, remember this easy method and you’ll have your answer in no time!
How do you teach comparing fractions Grade 5?
When teaching fractions, a common goal is for students to be able to compare fractions. This can be a difficult concept for students, especially those in grade 5. Here are a few tips to help you teach comparing fractions:
-Start by reviewing what a fraction is and what it represents. This will help lay the foundation for understanding how to compare fractions.
-Next, introduce the concept of equivalent fractions. Explain that when two fractions are equivalent, they have the same value even though they may look different. This is an important concept because it will allow students to see that there are multiple ways to represent a certain fraction. For example, 1/2 is equivalent to 2/4 even though they look different.
-Once students understand equivalent fractions, you can begin teaching them how to compare fractions. To do this, you can have students line up the fractions on a number line from smallest to largest or from largest to smallest. You can also have them use visual models such as fraction bars or circles to compare the sizes of the fractions.
-As with any new concept, it’s important to provide plenty of opportunities for practice. There are many websites and apps that offer games and activities specifically designed for practicing fraction comparison skills. You can also create your own practice problems.
-Finally, don’t forget to assess your students’ understanding periodically. This can be done informally through questioning during class or formally with a quiz or test.
Comparing fractions is an important skill for students to learn. By review basic fraction concepts, introducing equivalent fractions, and providing plenty of practice opportunities, you can help your students master this skill!
Conclusion
We hope this blog post “How Can I Find the Difference Between Two Fractions?” has helped clear up any confusion you may have had. If you have any further questions, feel free to reach out to us and we would be happy to help!
Hey, check out: How to Find Out How Much is 800 Square Inches in Width and Length in Feet and Miles
Today sponsors are Localhandymantulsa.com , sprinklerrepairlongisland.com , Mailboxrepairtulsa.com , Chestercountytowingservices.com and Huttotxroofrepair.com. Always providing the best services in town.