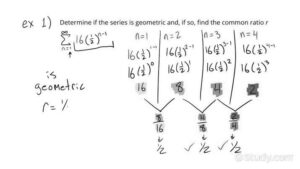
What is the constant ratio if the following series is geometric? Basically, a geometric sequence is one with a constant multiple preceding it. The constant ratio is usually identified by a variable called “r.”
When it comes to determining the constant ratio, it is important to remember that some sequences are not arithmetic or geometric, unless the first term is an integer. A geometric sequence is defined by a common difference between all terms. For example, the prime numbers are not a geometric sequence. Nevertheless, students should try to find a pattern in the sequence. In some cases, they may find the common ratio or difference by using subscripts.
In another case, an arithmetic sequence has a common ratio between its terms, and we can find it by using the term-to-term rule. To use this rule, we need to multiply the first term by the previous term. The next two terms will then be the common ratio. Then, we can calculate the constant ratio for the following geometric sequence, as follows:
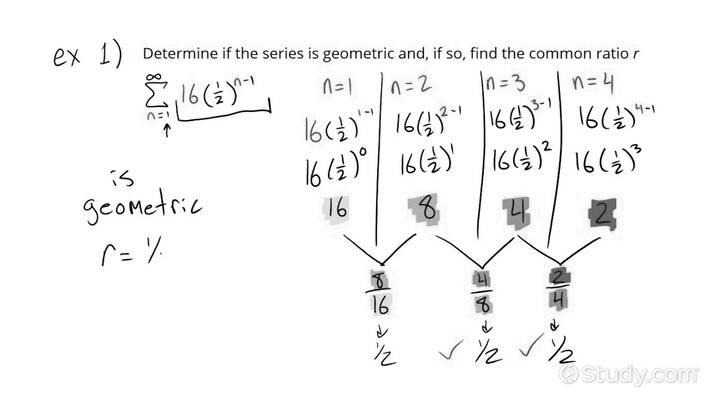
Figure 2: shows the graphs of the two sequences. Both sequences have a form of exponential function. However, one should not assume that (a) is geometric. If it is, then the constant ratio is rn-1. A geometric sequence, on the other hand, does not require dividing every term by the previous term. This is because the constant ratio will be a single term, rather than an exponential function.
Example:
Another example of a geometric sequence is the one in which r is a constant ratio between the first term and the common number. For example, if the first term and the common number of terms are equal, then n is the third term. In such cases, r is a fraction between -1 and 1.
In addition to the common ratio, a geometric sequence also has a non-zero constant between the first term and the last term. This ratio is called the constant ratio (CR). The common ratio can be obtained by dividing any term by the first term, which is a1 or a2.
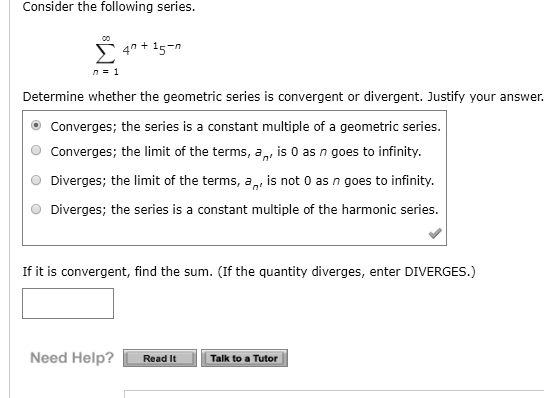
How do you find the constant ratio of a geometric sequence?
A geometric sequence is a sequence of numbers where each number is the previous number multiplied by a constant. For example, the sequence 2, 6, 18, 54 is a geometric sequence because each number is the previous number multiplied by 3.
To find the constant ratio of a geometric sequence, you need to divide each number by the previous number. In the example above, the constant ratio would be 3 because 2 divided by 6 is 3, 6 divided by 18 is 3, and 18 divided by 54 is 3.
What is the ratio of geometric?
What is the constant ratio?
There’s no such thing as a constant ratio – at least, not in the mathematical sense. A ratio is simply a comparison of two values, usually expressed as a fraction. For example, the ratio of a to b can be written as a:b. Ratios can be used to compare just about anything, from the lengths of objects to the amounts of ingredients in a recipe.
But what if we want to compare two values that are constantly changing? For example, let’s say we want to compare the value of a stock to the value of a currency. The stock might go up by 10% in a day, while the currency might go down by 5%. The next day, the stock might go down by 2% while the currency goes up by 3%. And so on.
In this case, we can’t just compare the two values at a single point in time, because the ratio is constantly changing. Instead, we need to calculate the average ratio over a period of time. This will give us a better idea of how the two values are related, on average.
To do this, we simply take the ratio at each point in time and then calculate the mean. For example, if we’re looking at the ratio of the stock to the currency over a five-day period, we would calculate the ratios for each day and then take the mean. This would give us a much better idea of the “constant” ratio between the two values.
What is the common ratio of the geometric series?
A geometric series is a series of numbers where each number is the previous number multiplied by a common ratio. For example, the series 2, 6, 18, 54, 162, 486, … has a common ratio of 3.
The common ratio of a geometric series can be found by taking any two consecutive terms in the series and dividing the later term by the former. For example, in the series 2, 6, 18, 54, 162, 486, … the common ratio can be found by dividing 18 by 6 to get 3.
The common ratio of a geometric series can also be found by taking the limit of the ratio of consecutive terms as the series goes to infinity. In other words, if you were to take the ratio of any two consecutive terms in the series and then take the limit as n goes to infinity, you would find the common ratio.
So, in summary, the common ratio of a geometric series is the number that each term in the series is multiplied by to get the next term. It can be found by taking any two consecutive terms in the series and dividing the later term by the former, or by taking the limit of the ratio of consecutive terms as the series goes to infinity.
What is the common ratio of the geometric sequence 5/15 45?
When we talk about the common ratio of a geometric sequence, we’re referring to the number that we multiply (or divide) by to get from one term to the next. In the sequence 5/15, 45, the common ratio would be 3. We can figure this out by taking any two adjacent terms and dividing them – in this case 15/5 = 3.
Now that we know the common ratio, we can use it to find any term in the sequence. For example, if we wanted to find the 100th term, we would just keep multiplying 3 by itself until we got to 100: 3 x 3 x 3 x … x 3 = 3^100. Then we would just multiply 5 by that number to get the 100th term: 5 x 3^100.
Of course, this only works for geometric sequences where the common ratio is a number (as opposed to a fraction or a decimal). But once you know the common ratio, it’s a quick and easy way to find any term in the sequence!
How do you find the geometric series?
A geometric series is a series where each successive term is obtained by multiplying the previous term by a common ratio. For example, the series 1, 3, 9, 27, 81, … is a geometric series with common ratio 3. To find the sum of a geometric series, one must find the value of the common ratio and then use the formula:
S = a1/(1-r)
where a1 is the first term in the series and r is the common ratio.
In the example series above, the common ratio is 3 and the first term is 1. Therefore, the sum of the series is
S = 1/(1-3)
which equals to 1.
Conclusion
We hope you enjoyed our latest post What is the constant ratio if the following series is geometric and found it informative. Be sure to check back soon for more great content.
Check out: What is the Measuring Unit of Pi?
Today sponsor is Infinity Charm. Check out these amazing magnetic heart bracelets! They are great for anyone who wants to show their love, or simply wants to add a little bit of flair to their outfit. They are stylish and unique, and would make a great gift for someone special. Also check out this very beautiful Magnetic Couples Heart Necklaces and this very nice Virgencita Necklace.