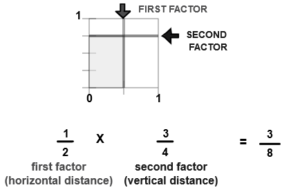
What is One-Third of a Quarter? To answer the question, “What is one-third of a quarter?” we first need to determine what the fraction is made of. One-third of a quarter is one-third of a quarter-hour. A quarter-hour is also one-third of a full-hour. To find the correct answer, we can use the following chart. First, consider the smallest fraction, one-third.
The fraction 1/4 is equal to 1/4 of a quarter. It equals one-half of a half-inch-thick piece of clothing. A quarter-inch-thick piece of cloth is one-half the length of a quarter-inch. In other words, a half-inch wide is equal to one-half-inch-long. Similarly, a quarter-inch wide shirt is one-quarter-inch wide.
In order to determine the larger fraction of a quarter, we need to know how many cents are in a quarter-inch. For instance, if one-third is equal to half-inch, then one-half is equal to three-quarters-inch. In most cases, one-third is equal to one-half. However, the smaller the denominator, the larger the fraction.
When we divide an hour into quarter-hours, we get fifteen-minute segments. One-third of an hour is twenty-five minutes, so a quarter-hour equals fifteen-minute segments. For example, a thirty-minute segment equals five, while a half-hour is forty-five minutes. The answer is fifteen-minute segments of a quarter-hour. Once we have established the ratio between the half-hour and quarter-hour, we can calculate the length of the quarter-hour portion of an hour.
How much is third quarter?
Is a third more than a quarter?
Is one third same as quarter?
It’s a common misconception that one third and a quarter are the same. Although they both involve division, they are actually two different concepts. One third is a fraction, while a quarter is an equal division.
To help understand the difference, let’s look at an example. Let’s say you have a pizza and you want to divide it equally between three people. You would cut the pizza into three equal pieces, giving each person one third of the pizza.
Now let’s say you have four people and you want to divide the pizza equally between them. You would cut the pizza into four equal pieces, giving each person a quarter of the pizza.
As you can see, one third and a quarter are not the same conceptually or mathematically. So next time someone tries to tell you that they’re equivalent, set them straight!
What is the fraction of one third?
When we talk about fractions, we’re usually talking about parts of a whole. For example, if I have a pizza and I want to share it with two other people, I would say that each person gets one third of the pizza.
But what exactly is one third?
One third is one part of something that has been divided into three equal parts. We can represent this fraction using a number line:
1| 2| 3
If we divide something into three equal parts, then each part is worth one third. So on the number line above, the point labeled “1” represents one third.
We can also represent one third using a fraction:
1/3
The top number (the numerator) tells us how many parts we have, and the bottom number (the denominator) tells us how many total parts there are. So in this case, we have 1 part out of 3 total parts.
We can also represent one third using a decimal:
0.333…
This is called a repeating decimal, because the 3 keeps repeating over and over again.
One way to think about fractions is that they’re like division problems. For example, if I want to divide something into three equal parts, I can write it as a division problem:
3 ÷ 1 = 3
The number on the left (the dividend) is telling me how many things I have, and the number on the right (the divisor) is telling me how many parts I want to divide those things into. So in this case, I have 3 things and I want to divide them into 1 part each. The answer tells me that each part will be worth 3 things.
Another way to think about fractions is that they’re like division problems with missing information. For example, if I know that each person gets one third of the pizza, but I don’t know how many people there are altogether, then I can write it as a division problem with a missing piece of information:
? ÷ 3 = 1
In this case, the question mark (?) represents the missing information. We don’t know how many people there are, but we do know that each person gets one third of the pizza. So if we divide the pizza into three equal parts, then each part will be worth one third.
One way to solve a division problem with a missing piece of information is to use estimation. For example, if I want to estimate how many people there are, I can look at the other two numbers in the problem and make a guess. In this case, I know that each person gets one third of the pizza, so I might guess that there are 3 people altogether:
3 ÷ 3 = 1
But I could also make a different guess, like 6 people:
6 ÷ 3 = 2
Or 9 people:
9 ÷ 3 = 3
It all depends on how much pizza there is!
Another way to solve a division problem with a missing piece of information is to use inverse operations. For example, if I want to find out how many people there are, I can multiply both sides of the equation by 3:
(? ÷ 3) × 3 = 1 × 3
? = 3
In this case, the question mark (?) still represents the missing information. We don’t know how many people there are, but we do know that each person gets one third of the pizza. So if we multiply both sides of the equation by 3, we can cancel out the division on the left side and solve for the missing information:
? = 3
In other words, there are 3 people altogether.
So when you see a fraction like 1/3, remember that it represents one part of something that has been divided into three equal parts. And if you ever need to solve a division problem with a missing piece of information, you can use estimation or inverse operations to find the answer!
What is 1/3rd called?
When we talk about fractions, we usually think of them as parts of a whole. For example, if I have a pizza and I cut it into 8 pieces, each piece would be 1/8th of the pizza. But what if we take a different perspective on fractions and think of them as division problems? For example, when we say that a piece of the pizza is 1/8th, we are really saying that if we divide the pizza into 8 equal pieces, one piece would be 1/8th of the total. So what is 1/3rd called?
If we think about 1/3rd as a division problem, then we are really saying that if we divide something into 3 equal parts, one part would be 1/3rd of the total. And just like with any other division problem, there is a name for this answer: it’s called the quotient. So in this case, the quotient would be 1/3rd.
But what if we want to think about fractions as parts of a whole again? In that case, 1/3rd would still be one part of the whole, but it would represent a smaller portion than it does when thinking about fractions as division problems. This is because when we think about fractions as parts of a whole, the denominator (the bottom number) tells us how many parts there are in total, regardless of the size of each part. So in this case, even though there are 3 equal parts, each part is smaller than it would be if we thought about the fraction as a division problem.
Whether you’re thinking about fractions as parts of a whole or as division problems, it’s important to be able to identify what 1/3rd is called. So remember: when you’re dealing with fractions, 1/3rd is called the quotient!
How many ⅓ make a whole?
If you’re anything like me, you were probably taught that there are three equal parts in a whole. So, it would make sense that if we put three of those parts together, we would get a whole, right? Well, it turns out that we would actually end up with more than a whole. In fact, if we have three ⅓ pieces, we would end up with 1⅓. Huh! Who knew math could be so confusing?
But wait, it gets even crazier. If we take three ⅓ pieces and add them to another whole piece, we would end up with 4⅓. So now not only do we have more than a whole when adding three ⅓ pieces together…we also have more than a whole when adding four ⅔ pieces together too!
So what’s going on here? How can this be? Let’s take a closer look at the fractions to see if that will help us make sense of things. When we have one whole piece, it is easy to see that it is made up of two halves or four quarters or eight eighths…and so on. And since each of those fractions are made up of smaller and smaller parts, it makes sense that when we add them all together, we would end up with more than a whole.
But what about when we have three ⅓ pieces? Well, each of those pieces is still made up of smaller parts…it’s just that there are now more parts in each piece. So when we add them all together, we end up with more than a whole because there are more parts in the sum than there are in one whole piece.
The same goes for four ⅔ pieces. Each of those pieces is made up of even more smaller parts than the three ⅓ pieces, so when we add them all together, we end up with even more than a whole.
So there you have it! Three ⅓ pieces or four ⅔ pieces will both give you more than a whole. And if you’re ever feeling like you need a little extra help making sense of fractions, just remember that it all comes down to the number of parts in each piece. The more parts there are, the greater the sum will be!
Is one third more than half?
Is one third more than half?
No, one third is not more than half. One third is less than half.
What is 1/3 in a decimal?
When we talk about fractions, we are talking about a part of a whole. A fraction is made up of two parts: the numerator and the denominator. The numerator is the number on top of the fraction line, and the denominator is the number on the bottom of the fraction line. The fraction 1/3 means that we have 1 part out of 3 equal parts. So, what is 1/3 in a decimal?
To convert a fraction to a decimal, we divide the numerator by the denominator. So, in our case, we would divide 1 by 3 to get 0.3333… This gives us our answer: 1/3 in a decimal is 0.3333….
It is important to note that when we divide 1 by 3, the division does not end after the third decimal place. In fact, if we were to keep going, we would find that the decimal repeats itself infinitely. This is because 3 does not divide evenly into 1 (there is always a remainder of 1).
When we write 0.3333…, the three dots (…) at the end indicate that the decimal keeps repeating. We could also write this as 0.33333… or 0.3 ( since every number after the decimal point is a 3). All of these numbers represent the same thing: 1/3 in a decimal form.
What is the percentage of ⅓?
There are many ways to express a number like ⅓ mathematically, but in fractions, it would be written as 1/3. The number 1/3 is equal to 0.33333333… when expressed as a decimal. In other words, 1/3 is 33.33% when rounded to the nearest whole percent.
What is 1/3 as a measurement?
When we talk about measurements, we are referring to the units of measurement that we use to quantify something. The most common units of measurement in the U.S. are inches, feet, yards, and miles for length; ounces, pounds, and tons for weight; and seconds, minutes, hours, days, weeks, months, and years for time. There are other less common units of measurement such as fathoms (for depth), nautical miles (for distance), and acres (for area).
But what if we want to be more specific with our measurements? For example, what if we want to know how long something is without using any unit of length? This is where fractions come in handy. We can use fractions to express a part of a whole or a quantity without using any unit of measure.
In this case, 1/3 as a measurement would represent one third of something – whether it be one third of an inch, one third of a foot, or one third of a mile. It all depends on what you’re measuring! So the next time you need to be more specific with your measurements but don’t want to use any units of measure, try using fractions instead.
What is 0.3 as a fraction in simplest form?
When we convert a decimal like 0.3 to a fraction, we are looking for what number we can multiply by 10, 100, 1000, etc. so that the result is equal to 3/10. In other words, we want to find what fraction is equal to 0.3 when both the numerator and denominator are multiplied by 10.
To do this, first write 0.3 as 3/10:
0.3 = 3/10
Next, multiply both sides of the equation by 10:
0.3 × 10 = (3/10) × 10
Now cancel out the common factors on each side of the equation and simplify:
3 30 300 3000
0.3 × 10 = (3/10) × 10 = —— = ——— = ———-=————
10 100 1000 10000
3 3
0.3 × 10 = (3/10) × 10 = —
10 10
As you can see, when we multiply both the numerator and denominator by 10, the decimal 0.3 changes to the fraction 3/10. So, in simplest form, 0.3 as a fraction is equal to 3/10.
How do you turn .33 into a fraction?
You can turn .33 into a fraction by dividing 33 by 100. This will give you the answer of 1/3.
Conclusion
We hope this blog post “What is One-Third of a Quarter?” has helped clear up any confusion you may have had. If you have any further questions, feel free to reach out to us and we would be happy to help!
Hey, check out: How Many Points Are in an Inch?
Today sponsors are Localhandymantulsa.com , sprinklerrepairlongisland.com , Mailboxrepairtulsa.com , Chestercountytowingservices.com and Huttotxroofrepair.com. Always providing the best services in town.