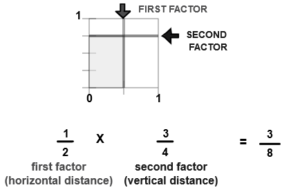
Comparing fractions can be a tricky business, but there are a few simple rules that can help make the process a little easier. The first thing to remember is that fractions represent a part of a whole, so the larger the fraction, the larger the part.
To compare fractions, you first need to find a common denominator. This is the lowest number that both fractions will divide into evenly. Once you have the common denominator, you can compare the numerators (the top number in a fraction) to see which fraction is larger.
For example, let’s say you’re comparing the fractions ¾ and 1/6. The common denominator here is 12, so when we compare the numerators, we get 9 (3 x 3) for ¾ and 2 (1 x 2) for 1/6. Because 9 is greater than 2, we can say that ¾ is larger than 1/6.
If you’re still having trouble comparing fractions, don’t worry – there are plenty of resources out there to help, including websites, apps, and books. With a little practice, you’ll be a pro in no time!
How do you compare fractions?
What are 4 ways to compare fractions?
When it comes to fractions, there are a few different ways to compare them. Here are 4 ways to compare fractions:
-
Compare by size
To compare fractions by size, you simply need to look at the numerators and denominators and see which fraction is larger. For example, if you’re comparing 1/4 and 1/3, you would look at the numerators (1 and 1) and see that they’re the same, and then look at the denominators (4 and 3) and see that 3 is larger than 4. Therefore, 1/3 is larger than 1/4.
-
Compare by converting to decimals
Another way to compare fractions is by converting them to decimals. To do this, you simply divide the numerator by the denominator. For example, if you’re comparing 1/4 and 1/3, you would divide 1 by 4 to get 0.25, and then divide 1 by 3 to get 0.333… Therefore, 1/3 is larger than 1/4.
-
Compare by converting to percentages
yet another way to compare fractions is by converting them to percentages. To do this, you simply multiply the fraction by 100. For example, if you’re comparing 1/4 and 1/3, you would multiply 1/4 by 100 to get 25%, and then multiply 1/3 by 100 to get 33.3333%. Therefore, 1/3 is larger than 1/4.
-
Compare by using a visual representation
A fourth way to compare fractions is by using a visual representation, such as a pie chart. To do this, you would simply draw out a pie chart with each fraction being a different color, and then see which fraction is larger. For example, if you’re comparing 1/4 and 1/3, you would draw a quarter of the pie chart one color and a third of the pie chart another color. It would be easy to see that 1/3 is larger than 1/4.
These are just a few of the ways that you can compare fractions. No matter which method you use, just be sure to be consistent so that you get accurate results.
How do you compare two fractions with different denominators?
When it comes to fractions, the denominator is what tells us how many parts the whole is divided into. The numerator is the number of those parts that we are interested in. That being said, in order to compare two fractions with different denominators, we need to find a common denominator between the two.
The least common multiple (LCM) is the smallest number that is a multiple of both denominators. To find the LCM, you can list out the multiples of each number until you find a common multiple. For example, if we are comparing the fractions ¾ and 5/6, we would list out the multiples of 3 and 6 like so:
3, 6, 9, 12, 15, 18
6, 12, 18
The LCM in this case is 18. This is because 18 is the smallest number that is a multiple of both 3 and 6. Now that we have a common denominator, we can compare the fractions by looking at the numerators. In this case, ¾ is greater than 5/6 because 3/18 is greater than 5/18.
It is worth noting that there is another method for finding the LCM, which is finding the greatest common factor (GCF) of the two denominators and then multiplying that by the denominator. In the example above, the GCF of 3 and 6 is 3, so the LCM would be 3 x 6 = 18.
Comparing fractions with different denominators can be a bit tricky, but as long as you find the LCM, it’s a piece of cake!
What fraction is bigger 2/3 or 3 4?
When it comes to fractions, the answer to this question depends on what you’re looking at. In terms of actual numbers, 3/4 is larger than 2/3. However, when you’re looking at the size of the fraction itself, 2/3 is larger.
It can be a bit confusing, but ultimately it all comes down to what you’re trying to compare. Are you looking at the actual numbers involved or the size of the fraction? The answer to this question will determine which fraction is bigger.
Which one is bigger 4 7 or 2 3?
If you’re anything like me, you might have trouble with math sometimes. I definitely do! But don’t worry, there’s an easy way to figure out which one is bigger between 4 7 and 2 3.
All you have to do is look at the first number in each pair. In this case, it’s 4 and 2. Since 4 is bigger than 2, that means 4 7 is the bigger pair.
See? That wasn’t so hard, was it? Now you can go forth and impress your friends with your knowledge of which one is bigger between 4 7 and 2 3!
Which fraction is bigger 4 5 or 2 3?
When it comes to fractions, the bigger number is not always the bigger fraction. In the fraction 4/5, the numerator (4) is bigger than the numerator (2) in 2/3. However, this does not mean that 4/5 is necessarily the bigger fraction.
To find out which fraction is bigger, we need to look at the denominators. The denominator is the number on the bottom of the fraction and represents how many parts the whole is divided into. In this case, 5 is divided into 4 parts and 3 is divided into 2 parts.
When the denominator is the same, the fraction with the bigger numerator is the bigger fraction. However, when the denominators are different, we need to find a common denominator. The common denominator is the lowest number that both denominators will go into evenly.
In this case, the common denominator is 15. To find the equivalent fractions with a common denominator, we need to multiply the numerator and denominator of each fraction by a number that will give us the common denominator.
For 4/5, we multiply 4 by 3 and 5 by 3 to get 12/15. For 2/3
Which fraction is greater I 3/5 or 2 3?
When it comes to fractions, there is a general rule of thumb that the larger the numerator is in relation to the denominator, the larger the overall value of the fraction will be. However, there are exceptions to this rule. In the case of 3/5 and 2/3, both fractions have a numerator that is larger than the denominator. However, 3/5 is the larger of the two fractions.
To understand why, it helps to think about fractions as division problems. 3/5 can be thought of as 3 divided by 5, which equals 0.6. 2/3 can be thought of as 2 divided by 3, which equals 0.6666… When you divide 3 by 5, you get a decimal answer that is less than 1. When you divide 2 by 3, you get a decimal answer that is greater than 1. Therefore, 3/5 is less than 2/3, and 2/3 is the greater of the two fractions.
Which fraction is bigger 5 by 7 or 3 by 4?
There are a lot of different ways to compare fractions, but in this blog post, we’re going to compare fractions by looking at the numerator and denominator. In other words, we want to know which fraction has a bigger numerator, and which fraction has a bigger denominator.
When we compare the fractions 5 by 7 and 3 by 4, we can see that 5 is bigger than 3, and 7 is bigger than 4. Therefore, the fraction 5 by 7 is bigger than the fraction 3 by 4.
Which fraction is bigger 5 7 or 2 3?
For a long time, I always thought that the answer to this question was 5/7 because it was the larger number on top. However, I recently learned that this isn‘t always the case and that the answer to this question is 2/3. The reason for this is because when you‘re working with fractions, you‘re really looking at the value of each number in relation to one another. In this case, 5/7 and 2/3 are both equal to 10/21. So, really, the answer to this question depends on what you‘re looking for. If you‘re looking for the larger number, then the answer is 5/7. However, if you‘re looking for the value that‘s actually larger, then the answer is 2/3.
Conclusion
We hope this blog post “Comparing Fractions” has helped clear up any confusion you may have had. If you have any further questions, feel free to reach out to us and we would be happy to help!
Hey, check out: What is Half of 21 5/8?
Today sponsors are Localhandymantulsa.com , sprinklerrepairlongisland.com , Mailboxrepairtulsa.com , Chestercountytowingservices.com and Huttotxroofrepair.com. Always providing the best services in town.